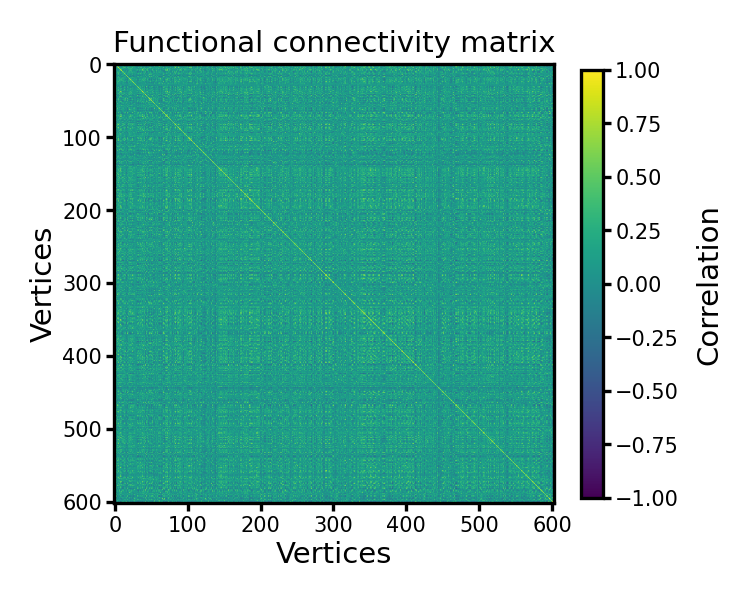
Functional connectivity#
Functional connectivity measures to what extent two brain regions are synchronized with each other. It is usually quantified using the Pearson correlation between their time series.
import numpy as np
import neuroboros as nb
from scipy.spatial.distance import pdist, cdist, squareform
from scipy.stats import pearsonr
import matplotlib.pyplot as plt
dset = nb.Budapest()
sids = dset.subjects
dm_ico32 = dset.get_data(sids[0], 'budapest', 1, 'l')
dm_ico32.shape
(598, 9675)
In this example, we compute fine-grained vertex-by-vertex connectivity.
To avoid a large amount of computations, we downsample the data matrix from ico32 resolution (10,242 vertices prior to masking) to ico8 resolution (642 vertices prior to masking).
xfm = nb.mapping('l', 'onavg-ico32', 'onavg-ico8', mask=True)
xfm.shape
(9675, 603)
dm = dm_ico32 @ xfm
print(dm_ico32.shape, xfm.shape, dm.shape)
(598, 9675) (9675, 603) (598, 603)
Using xfm obtained from nb.mapping, the data matrix is downsampled from 9675 vertices to 603 vertices.
The connectivity matrix has the shape of \(n_v \times n_v\), in this case, it’s 603×603.
Note that different from computing RDM, here we use the transpose of dm (dm.T)instead of dm itself.
Each entry in the functional connectivity matrix is the correlation between two vertices’ time series, and therefore it’s one minus correlation distance:
d = pdist(dm.T, 'correlation')
mat = 1 - squareform(d)
print(d.shape, mat.shape)
(181503,) (603, 603)
fig, ax = plt.subplots(1, 1, figsize=[_/2.54 for _ in [6, 6]], dpi=300)
im = ax.imshow(mat, vmax=1, vmin=-1, cmap='viridis')
ax.set_title('Functional connectivity matrix', size=7, pad=3)
ax.tick_params('both', labelsize=5, size=2, pad=1)
ax.set_xlabel('Vertices', size=7, labelpad=1)
ax.set_ylabel('Vertices', size=7, labelpad=1)
cb = fig.colorbar(im, ax=ax, shrink=0.8)
cb.ax.tick_params(labelsize=5, size=2, pad=1)
cb.ax.set_ylabel('Correlation', size=7)
plt.show()